Complete Program

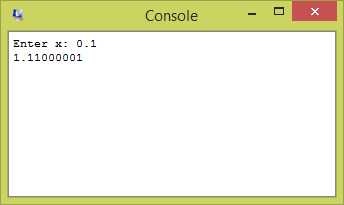
As we have seen before, the results are not quite accurate. You would expect this because 0.1 cannot be represented accurately.

Here is the complete program, suitable for you to copy into a text editor and to play with:

## float1.asm -- compute ax^2 + bx + c for user-input x 
##
## SPIM settings: pseudoinstructions: ON, branch delays: OFF,
##                load delays: OFF

        .text
        .globl main

        # Register Use Chart
        # $f0 -- x
        # $f2 -- sum of terms

main:   # read input
        la      $a0,prompt          # prompt user for x
        li      $v0,4               # print string
        syscall
        
        li      $v0,6               # read single
        syscall                     # $f0 <-- x
        
        # evaluate the quadratic
        l.s     $f2,a               # sum = a
        mul.s   $f2,$f2,$f0         # sum = ax
        l.s     $f4,bb              # get b
        add.s   $f2,$f2,$f4         # sum = ax + b
        mul.s   $f2,$f2,$f0         # sum = (ax+b)x = ax^2 +bx
        l.s     $f4,c               # get c
        add.s   $f2,$f2,$f4         # sum = ax^2 + bx + c
        
        # print the result
        mov.s   $f12,$f2            # $f12 = argument
        li      $v0,2               # print single
        syscall

        la      $a0,newl            # new line
        li      $v0,4               # print string
        syscall

        li      $v0,10              # code 10 == exit
        syscall                     # Return to OS.
        
##
##  Data Segment  
##
        .data
a:      .float  1.0
bb:     .float  1.0
c:      .float  1.0

prompt: .asciiz "Enter x: "
blank:  .asciiz " "
newl:   .asciiz "\n"