created 01/01/03; edits 11/11/12, 03/25/16
Rewrite the TriangleTester program described in the chapter so
that the user is asked for N and that the value entered is
tested to make sure it is positive.
Click here to go back to the main menu.
Rewrite TriangleTester so that Triangle()
is a static method of that class.
Eliminate the TriangleCalc class.
(Include user input from exercise 1, if you want.)
Click here to go back to the main menu.

Write a program that implements this definition of square numbers:
square(1) = 1 square(N) = square(N-1) + 2N -1
Make a complete program similar to TriangleTester.java given in the chapter.
Aside: where did this crazy definition of square come from?
Easy: this is just algebra:
(N-1)2 = N2 - 2N + 1
rearrange to get:
N2 = (N-1)2 + 2N - 1
Another way to think of this is a square number gives the total number of pins in a square arrangement of pins with N pins on a side. Draw a square with four dots (pins) on a side. Then expand the square so that it has five dots on a side. Using your picture, explain why the recursive definition of square numbers is correct.
Square numbers are also mentioned in the quiz for this chapter.
Click here to go back to the main menu.
Write a program that implements this definition of
log base 2 for positive integers N:
log(1) = 0 log(N) = 1 + log(N/2)
Use only integer math for this. Of course, you will not get the same value as given by log function for floating point math. The integer log function is useful when dealing with things that do not exist in fractional amounts.
Compute log(32) using this method. You should find that log(32) = 5. Draw a diagram similar to the one on page 17 of this chapter that shows how this works. You will also find that log(48) = 5. You may be less than happy with this result, but when calculations are restricted to the domain of integers this is the best you can do.
Click here to go back to the main menu.
Write a program that implements this definition of
pow base 2 for positive integers N:
pow(0) = 1 pow(N) = 2*pow(N-1)
Use only integer math for this.
You should find that pow(5) = 32.
So pow( log(32) ) = 32.
Sadly, pow( log(48) ) = 32.
Click here to go back to the main menu.
A pentagonal number is one that corresponds to dots arranged into a pentagon. Here are the first four pentagonal numbers and their pentagons:
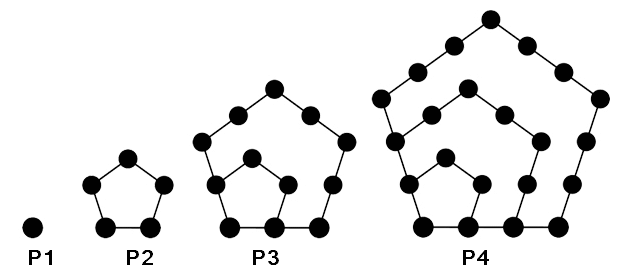
The pentagonal number PN has sides made of N dots. When you count the dots for a pentagonal number include the dots for the inner pentagons. So to figure out how many dots PN has, find out how many does P(N-1) has and add the dots for the new sides of size N.
P1 = 1, P2 = 5, P3 = 12, P4 = 22
Figure out a recursive formula for PN and then write a program that implements it.
Click here to go back to the main menu.